Binary-Search (二分搜尋法)，是一種針對已經排好序的區間內， O(logN) 的搜索方式。 Binary-Search 在處理邊界時很容易出錯。 基本上都是沒注意到兩大原則 :

• 每次都一定要縮減收所區域
• 每次縮減不能排除潛在答案

雖然淺顯易見，但實踐在寫的時候還是常常會寫出 bug 。

Binary-Search 最簡單的形式如下，是一個找精確值的模板

// int[] arr = {1, 2, 3, 4, 5, 6, 7}
// k = 3
public init binarySearch(int[] arr, int k){
    int l = 0;
    int r = arr.length - 1;
    while(l <= r){
        int mid = l + (r - l) / 2 ; // avoid overflow
        if(arr[mid] == k){
            return mid;
        } else if (arr[mid] > k){
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }
}

但情境變化一下

• int[] arr = {1, 2, 2, 5, 5, 6, 7}，找最接近4的數
• int[] arr = {1, 2, 3, 5, 5, 6, 7}，找比4大最小的數

就不能套用了。故接下來思考一下一個比較 general 模板，並深入分析下。

Binary-Search 本質

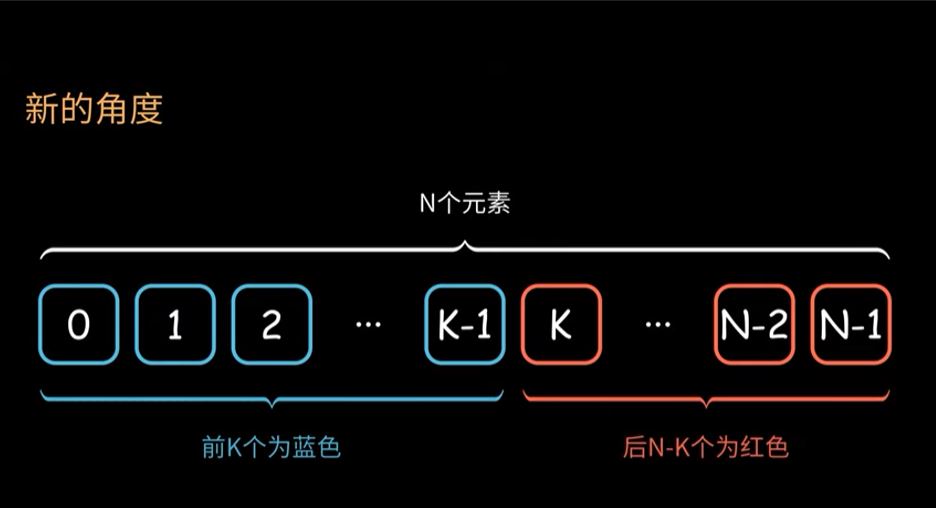
使用 Binary-Search 找所謂的解答，可以想成是要找藍紅邊界K，這邊可以由圖像了解 Binary-Search 高效快速的原因，就是當 Binary-Search 找到某個位置為藍色，則它前面的位置一定皆為藍色，故可以直接把左指針拓展到元素所在位置。同理紅色也是一樣思考方式。

分析驗證

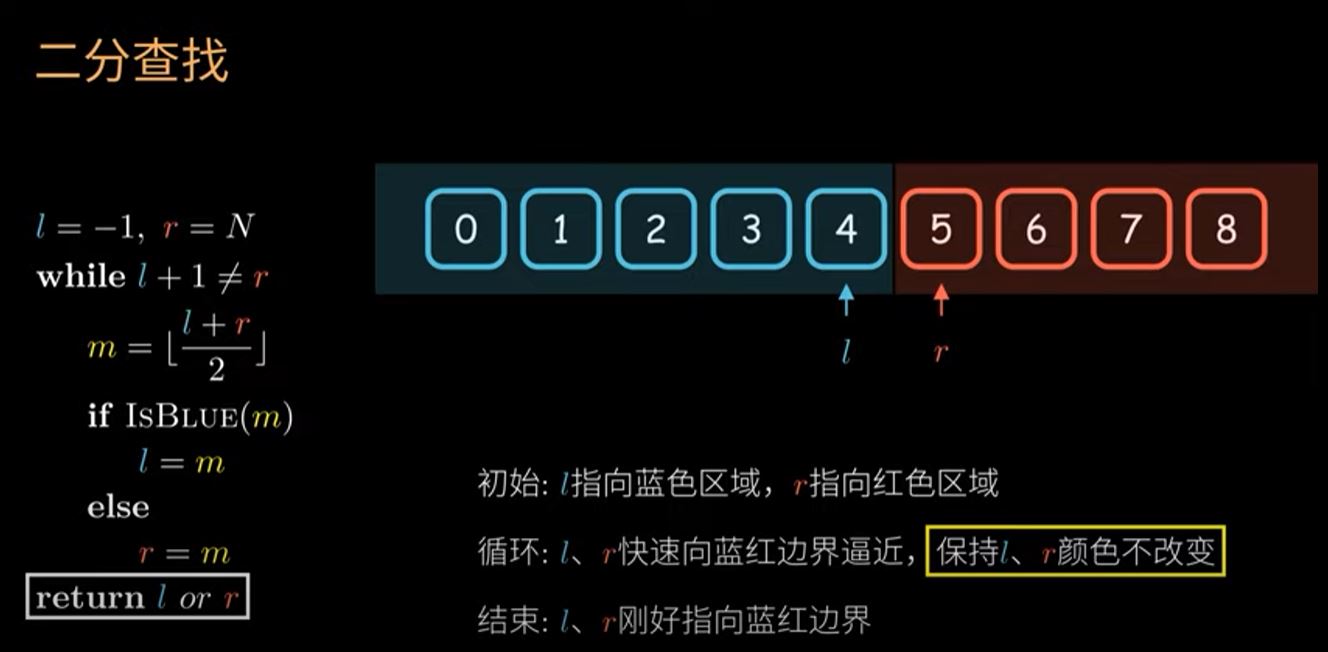
接下來使用圖像說明，整理並分析一個 Binary-Search 通用的模板:

為什麼初始 l = -1 , r = N ?

試想一下，假如 l = 0，但整個 arr 都是紅色，那就和 l 代表的意義矛盾了，因為 l 的意義是在它當下位置，以及之前的位置，全部都是藍色。

同理若整個 arr 都是藍色，若讓 r = N-1，也和 r 代表的意義矛盾了。

中間點 m，是否一直都會在 [0, N-1] 內呢?

看一下 m 的下界，由於 m = (l + r) / 2 ，所以要讓 m 最小，我們要找 l 最小和 r 最小。

看一下 m 的上界，要讓 m 最大，我們要找 l 最大和 r 最大。

更新指針時，能不能寫成 L = m+1 或 r = m-1 ?

很多二分查找模板都會有類似的部分，但這邊統一寫成 l = m , r = m。 可以試想假如某自迴圈，m 剛好指向藍色地的邊界最後一個元素，若再用 L = m+1 ，就會越界了。

有沒有可能死循環 ?

• l + 1 = r 會退出 loop ， 不用擔心

• l + 2 = r 這時候會發現 m 剛好是在 l 和 r 中間，接下來因為 l = m 或 r = m，故都會回到 l + 1 = r 這個 case。

• l + 3 = r 會回歸到 l + 1 = r case 或者 l + 2 = r 這個 case

故以上分析，其實最後都會回到 l + 1 = r ，然後退出 loop， 不用擔心死循環的。