在刷 leetcode 時，都會需要分析和解釋一下自己寫的程式的演算法複雜度，基本上主要是解釋 :

  • 時間複雜度
  • 空間複雜度

從以上兩個面相去分析 code 效率、品質、trade off，本文記錄一些分析要點。另外建議面試的時候，當對題目有想法時，先不用急著直接實作，而是先估出複雜度，並和面試人討論，確認不會 TLE ；空間是否需要優化；符不符合題目要求等等，最後再開始寫。

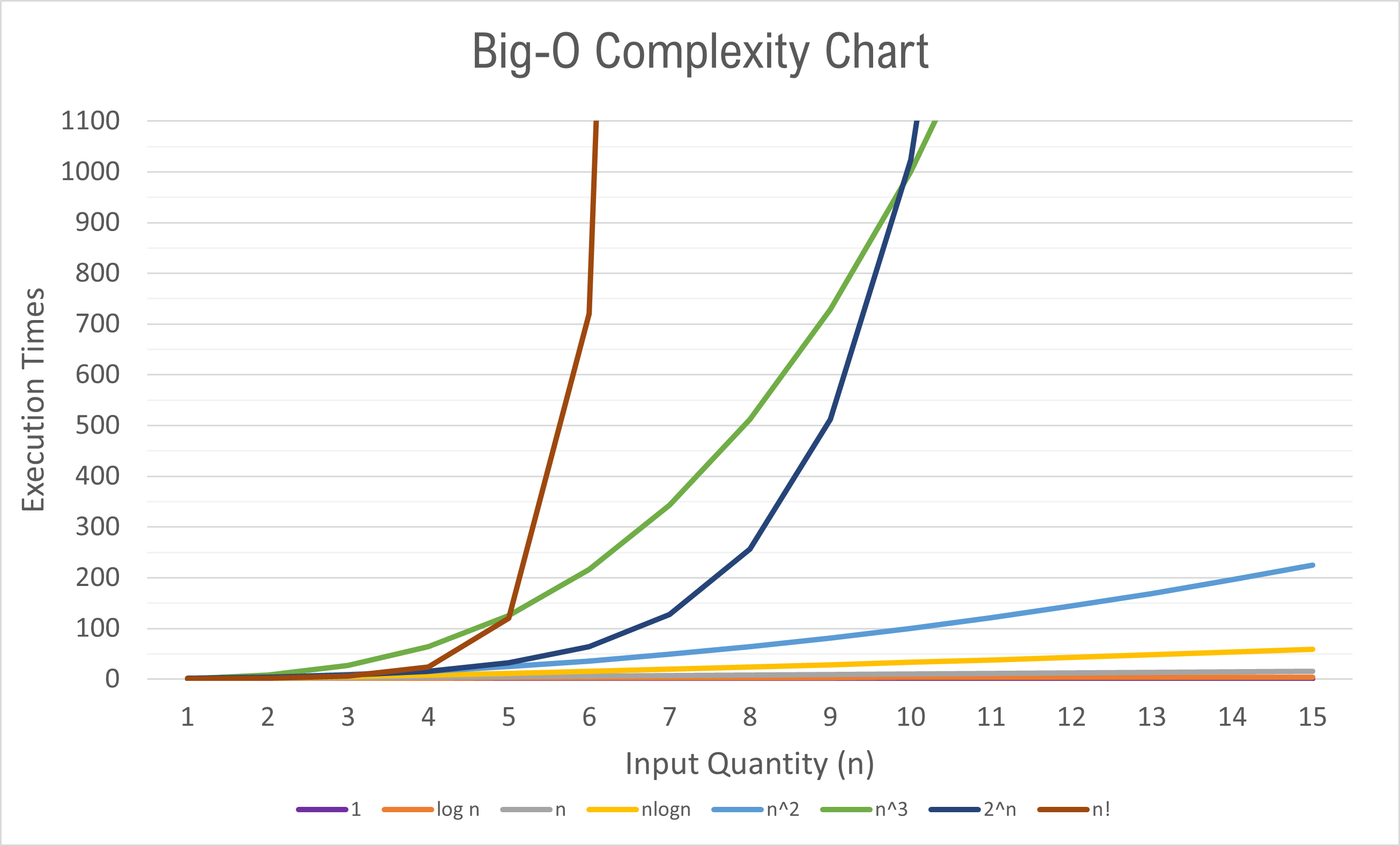
Complexity 是用來形容某個函數和它的參數間的關係，最常用的表示方法是 Big-O notation，代表演算法函數的 Upper bound 。 其值有一種簡單的估算方法 :

  • 函數除了最高次項以外都去掉
  • 然後再把最高次項的係數去掉
  • Log 底數忽略不計

得到的結果，就是演算法的複雜度答案了。

大寫的英文字母 O 函數，代表演算法執行步驟數目上限

時間複雜度(Time Complexity)

想要描述一個演算法執行速度有多快，直覺的方式是測量時間。但是由於執行時間深受機器規格與實作方式影響，故傾向的分析是統計演算法步驟數。

  • Recursion tree的時間複雜度，主要注意節點的單一子問題代價，是指每次函數執行中，除去遞歸調用以外的代價。明確了單一代價，整個遞歸樹的總代價就可以計算了，就是樹中所有節點的代價和。

空間複雜度(Space Complexity)

計算演算法執行時所花費的記憶體空間成本，也就是stack、heap、memory。空間複雜度可分為幾個部份來分析：

  • Fixed part：對於一些程式常數、基本變數所需要的儲存空間。
  • Input Output part：存儲 input data 所需的空間和最後答案的 data，通常這些部分不包括在空間複雜度的計算中，因為這是解決問題所必需的。
  • Variable part：演算法執行過程中額外使用的空間。
  • Recursion tree stack：如果使用recursion，則還需要考慮遞迴調用所使用的棧空間。

在 leetcode 中演算法討論中，空間複雜度時，專注在 Variable part 和 recursion tree stack 就可以了

Example

假設 n 為足夠大時 : 1 < logn < n < nlogn < n^2 < 2^n < n!

如上圖所示，可以知道 Big-O 複雜度越高，隨著數據規模增長，效率就會越來越差，因此 n 越大時，寫好演算法就越重要。

  • Leetcode 509 Fibonacci

    public static int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

    可以參考自己的 leetcode 509. 有詳細分析

    • 時間複雜度: O(((1+(根號5))/2)^n)

    • 雖然樹中至多有 2^n 個節點，但任何給定時間頂多只會有到最大深度 n 個節點，故空間複雜度是 O(n)

  • LeetCode 206 Reverse Linked List

    • Fixed part：遞迴解法中，我們用到了一個局部變數 p 來存儲遞迴調用 reverseList(head.next) 的結果。這是常數空間 O(1)

    • input output part：輸入是一個鏈表，通常這部分不包括在空間複雜度的計算中。

    • Variable part：演算法沒有使用任何額外的結構（如陣列或字典等）來儲存，所以輔助空間是 O(1)

    • recursion stack：演算法的遞迴深度和鏈表的長度 n 成正比。深度會是O(n)

一般來說​「時間複雜度」與「空間複雜度」之間是可以相互 trade off 的！例如說 :

  • Bubble Sort 就不需要額外的記憶體空間，但是做起來比較久
  • Bucket Sort 就需要額外的記憶體空間，但是做起來比較快。

Big O Notation 表格

Big O Notation別名常見演算法
O(1)常數Array 讀取
O(n)線性Linear search
O(log n)Logarithmic二分搜尋法
O(n log n)線性對數堆積排序，合併排序
O(n^2)平方氣泡排序，插入排序
O(n^3)三次方三重迴圈
O(2^n)指數費氏數列
O(n!)階層排列組合，八皇后問題

參考資料