Varint & Zigzag Encoding
蠻多 coding 語言在一般情況下是使用
32 bits的空間來儲存整數的,例如 Java 的 int,範圍是-2147483648 ~ 2147483647,大約正負21億。但是現實世界中,較小的數字往往比較常出現,大約幾十到幾十萬是最多最常出現的,如果只是要儲存或傳輸這樣的一個小數字,卻每次都需要用到 32 bits 的空間,其實有點浪費,這是有機會優化的 !Varint 和 Zigzag 演算法就是要處理這種問題,讓值小的數字,可以用較少的 byte 數量表示,而達到資料壓縮目的,著名的資料傳輸格式 Protobuf 也是通過 Varint 和 Zigzag ,來大幅減少了資料佔用的空間。
前備知識 - 負數的二進位表達
複習一些知識,二進位表達負數的方法有三種:
- Signed Magnitude:
用第一位 bit 來表達正負數,0 為正,1 為負 - 1’s Complement:
就是取補數,0、1 交換 - 2’s Complement:
常稱為二補數,0、1 交換後,還要在 + 1
2’s Complement 為目前用來表達負數二進制的方法
原因是 Signed Magnitude 和 1’s Complement 都有極大的缺點:
- Signed Magnitude 加減等運算時的複雜較高
- 1’s Complement 會發生不唯一的
「0」,因為有+0和-0這樣的表示
Varint
全名稱是 Base 128 Varints,接下來直接用範例展示 Varint Encoding 流程,我們以 int32 資料類型,數字 300 來當例子,直接展示 Varint 過程:
300
= 256 + 32 + 8 + 4
= 0000 0000 0000 0000 0000 0001 0010 1100 (二進制)
= 0000 0000000 0000000 0000010 0101100 (每7位一組)
= [000]0000 0000000 0000000 0000010 0101100 (把 0 補滿)
= 0101100 0000010 (低位換到前面,全 0 的 byte 捨棄)
= `1`0101100 `0`0000010 (按規則最前面補 1 或 0)
# 承上知道 300 需要 2 bytes 來表示
其中比較特別的是按規則最前面補 1 或 0,那到底是甚麼規則呢? 規則是 :
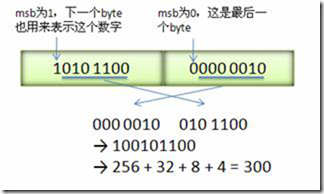
1: 表示後續的 byte 也是數字的一部分0: 表示本 byte 是最後一個字節,剩餘 7 位都用來表示數字的值。
最前面補 1 或 0,其含義只是代表著一個標識位而已,代表後面有沒有繼續接上數值。由於是在每個 byte 的最高位的英文是 most significant bit,故也會簡寫成 msb。為了更好理解,這規則由下圖補充展示:
由於流程中有低位換到前面的操作,這也表明 varint 編碼後的資料的位元組是小端序排列的。這樣做的原因是解碼的過程比較高效,可以先把小數字部分解碼出來的二進制位先放在低位,之後比較大的數字解碼出來的二進制,直接往後放到高位就可以了。
承上流程,可知這是一種自帶分隔符號的編碼方式,除了標識位,剩餘 7 bit 會存放真實資料的部分,而 2^7 = 128 剛好,所以才會使用 Base 128 Varints 這種命名。在實際場景中,小數字的使用率遠遠多於大數字,因此通過 Varint 編碼對於大部分場景都可以起到很好的壓縮效果。
由上述過程,我們也可以發現,若把 int32 升級到較大的整數類型 int64,也不影響 Varint Encoding 結果,這也表示有比較好的兼容性。
Zigzag
ZigZag 的編碼方式會把整數重新排列,變成 0, -1, 1, -2, 2,... 這樣來來回回的數字序列,這種之字形樣子,就是 zig-zag 的名字由來。而它的的出現,是為了解決 Varint 對負數無法有效壓縮的問題。由於負數的二進制表示法會很多 1,若對負數直接使用 Varint 編碼,總是會佔用較多的 bytes,例如 int32 資料類型,數字 -2 來當例子,推導如下:
-2
= 1111 1111 1111 1111 1111 1111 1111 1110 (2 的 int32 表示,取 Complement + 1)
= 1111 111111 111111 111111 1111110 (每7位一組)
= 0001111 111111 111111 111111 1111110 (補 0)
= 1111110 111111 111111 111111 0001111 (低位在前,沒有全0的,所以沒有捨棄)
= `1`1111110 `1`111111 `1`111111 `1`111111 `0`0001111 (第8位按規則補 1 或 0)
# 承上知道 -2 需要 5 bytes 來表示
原本 -2 用單純 int32 表示就是固定 4 個 bytes;使用 Varint 後反而變 5 個 bytes,反而浪費更多空間
ZigZag 的作法是把數字依照絕對值大小排序,觀察數字和順序其二進位的關係 :
| num | num的二進位 | 順序 | 順序的二進位 | 順序的二進位,記號要去除的最後一位 |
|---|---|---|---|---|
| 0 | 00000000 | 0 | 00000000 | 0000000[0] |
| -1 | 11111111 | 1 | 00000001 | 0000000[1] |
| +1 | 00000001 | 2 | 00000010 | 0000001[0] |
| -2 | 11111110 | 3 | 00000011 | 0000001[1] |
| +2 | 00000010 | 4 | 00000100 | 0000010[0] |
| -3 | 11111101 | 5 | 00000101 | 0000010[1] |
| +3 | 00000011 | 6 | 00000110 | 0000011[0] |
如何建立 (num -> 順序) 的函數 F 映射呢 ? 表中可以觀察到 :
- 若將順序的二進位表示中的最後一個 bit 當成 signed bit 移除掉之後
- 承上作法後,看剩下的 bits :
- 對於 num 是正數: 和原本數字二進位表示基本一樣,只差一位而已
- 對於 num 是負數: 取 Complement 後,和原本數字二進位表示基本一樣,也只差一位而已
- 承上操作結果,最後在把移除掉的 signed bit 加回最後面位置,就發現完全一樣了
實際操作如下(簡單用 1 個 byte 來說明) :
+3 = 00000011
= 0000011x(左移一位)
= 00000110(補上 signed bit。因 3 的順序是 6 ,6 signed bit 是 0,故補上 0)
= 6
-3 = 11111101
= 1111101x(左移一位)
= 0000010x(因為是負數還要多取 Complement)
= 00000101(補上 signed bit。因 -3 的順序是 5 ,5 signed bit 是 1,故補上 1 )
= 5
因此我們只要
- 把原數字二進位表示左移一位
- 若是負數還要再多取 Complement
- 最後將 signed bit 補到最後一位
就是我們要的結果! 這過程的函數化詳細說明請參考 reference,以下直接附上 32bits 轉換公式:
func int32ToZigZag(n int32) int32 {
return (n << 1) ^ (n >> 31)
}
心得
會介紹 Varint & Zigzag 主要是因為 Protobuf 就是透過這些演算法來壓縮資料。資料傳輸的時候出於 IO 的考慮,我們會希望盡可能的資料壓縮,而 Varint 就是一種對數字進行壓縮的方法,但 Varint 也是有缺點的,就是對負數壓縮很差,故還可進一步使用 ZigZag 編碼解決負數的壓縮問題。
如果提前知道 Protobuf 該 field 的值,有部分會是取負數的時候,可採用 sint32/sint64 類型,而不要使用 int32/int64。因為採用 sint32/sint64 數據類型表示負數時,會先採用 Zigzag 編碼再採用 Varint 編碼,從而更加有效壓縮數據。