206. Reverse Linked List
反轉 Linked List 是一道經典的題目,可以用分別用 :
- 指針 (iterative)
- 遞迴 (recursive)
兩種截然不同的風格來解答。個人認為是蠻好的題目,可以多寫幾次,並從各種不同的解答方式來說明思考,故在此筆記。要說簡單也不算,對於 recursive 解法一開始我覺得有點難理解 ! 雖然被歸類在 Easy,但我私心覺得蠻容易打擊第一次做的人的…
思路
從指針角度做反轉的話,概念是使用座標紀錄點,分別代表
- 「未來」的 next 指針;基本上要最先標定未來座標紀錄點,以免當前狀態經過操作後會丟失前往 next 的能力。
- 「過去」的 pre 指針;
pre = cur表示 pre 可藉由 cur 座標紀錄點來到現在狀態 - 「現在」的 cur 指針;
curr = next,因為一開始就有先創造未來座標紀錄點,所以 curr 可以到 next
另外有些小重點 :
因為 Linklist 最終必須結束於 null,故我們都會創造一個
pre = null,擔任這個反轉過後的結束狀態。最後 cur 是指向 NULL的,而 pre 才是指向反轉後的第一個 node,因此回傳的指標是 pre 而不是 cur。
解答
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode pre = null;
ListNode cur = head;
while(cur != null){
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
return pre;
}
}
雖然這題也可以直接操作 head 來得到解答,但這並不是一個好的習慣 ! 因為如果直接操作 head 的話,就會丟失原始 head 的最開頭狀態訊息。很多題目都還會需要在參考原初的訊息,故還是推薦創造一個 cur 指針來遍歷會比較好 !
// 不推薦這樣寫
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
while(head != null){
ListNode next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}
}
思路
使用遞迴需要滿足以下條件:
- 問題解可以分為幾個子問題解
- 問題和子問題,求解思路完全一樣
- 存在遞迴終止條件 (base case)
遞迴問題中,定義出終止條件非常重要,以本題為例,當走到最後一個節點時,就不需要再往後處理,而這個節點就會是新的 head 節點,應該將新頭節點回傳。
思考遞迴時,都從一個中間狀態去思考,假設節點 N 後面都反轉完成了,那我們在 節點 N 要做什麼事情呢 ? 要做 :
- 首先要把節點 N 後面的那個已經反轉完成的節點,指向自己這個節點 N :
(N node).next.next = (N node) - 節點 N 本來指向的下一個節點的路,要把它斷掉 :
(N node).next == null
解答
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode reversed = reverseList(head.next);
head.next.next = head;
head.next = null;
return reversed;
}
}
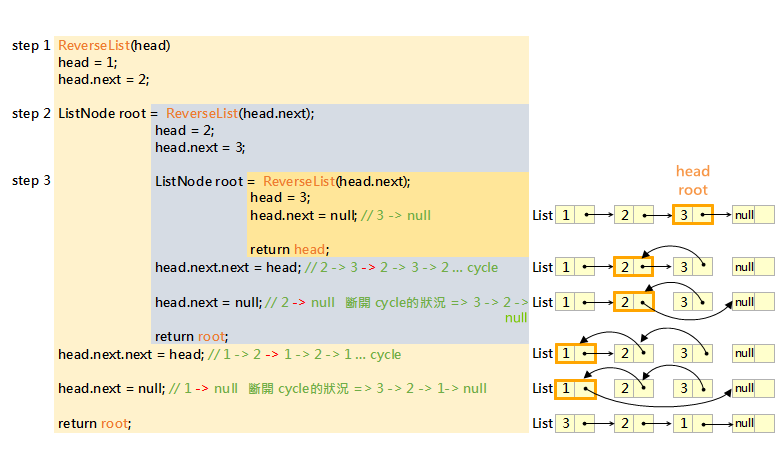
再次觀察並思考上述解答,其實可以發現:
reversed這個是指原本 Linked List 最後一個 Node,故解答要返回的是反轉後的 head,而不是節點 N- head 的下一個 Node 的 next ,指向 head 本身,這個相當於把當前正在進行的結點,變成反轉後 Linked List 最尾 Node
- 因為是回溯的操作,所以當前正在進行的結點的下一個結點,總是在上一輪被移動到最尾了
- 最後再把前正在進行的結點,連結到下一個節點的路徑切斷。若沒有這一個操作,例如要反轉,
1 -> 2 -> 3,最後會得到3 -> 2 <-> 1,在反轉的鏈表的末尾得到一個循環,當試圖遍歷這個鏈表時,會陷入無窮循環
一般對於 Linked List 都是使用 Bottom up recursion,因為 Recursion 其實是 call stack 概念,是先進後出的概念,這個對於解從後往前的 Linked List 題目非常適合。
時間空間複雜度
時間複雜度 : O(N)
要使 linked list 反向,假設有 N 個 node,不論是 iterative 或 recursive 的方法都需走訪每個 node 並改變他們所指向下一個 node 的指標,所以時間複雜度為
O(N)。
空間複雜度 : 兩種解法不太一樣
對於指標 iteratively 的方法,由於整個演算法只需要存指標空間,故為
O(1)對於 recursive 的方法:
在這題遞迴的情境下,recursion tree 中每一個 Node 都對應一個未解決的遞迴呼叫,這些呼叫會一直留在 Stack 中直到它們被解決。而這題 recursion stack 的最大大小剛好等於 recursion tree 中 Node 的數量,這也就是
N。並且解法中, 每個 Node 內並沒有使用額外空間儲存資料,所以其複雜度為常數。綜合上述, recursive 的空間複雜度為
O(N*1) = O(N)
一般來說,在分析遞迴的空間複雜度時,常關注的是遞迴呼叫所使用的 Stack 空間,這通常是主要的空間消耗原因之一。在這種簡單的遞迴情境下,直接說空間複雜度是由於遞迴呼叫的數量決定的,所以是O(N),通常會更簡單和直觀。