39. Combination Sum
這題給了一個 array of distinct integer 以及目標總和 target , 求用此 array 來組成目標數字的所有組合。像這種要求返回所有符合要求解的題目,基本都是要利用到遞迴,類似的題目有 Subset 、 Permutation 、 Combination 等等,解題套路都是使用 DFS 和 Backtrack 來求得答案。
思路
這也是蠻典型的 backtracking 題目,有些值得注意的題目說明和隱含意義:
The same number may be chosen from candidates an unlimited number of times這表示不限制使用 candidates 內 element 的使用次數
return a list of unique combinations此題要求的答案是數字組合,並非排列,故暗示了數字順序不重要這個 hint
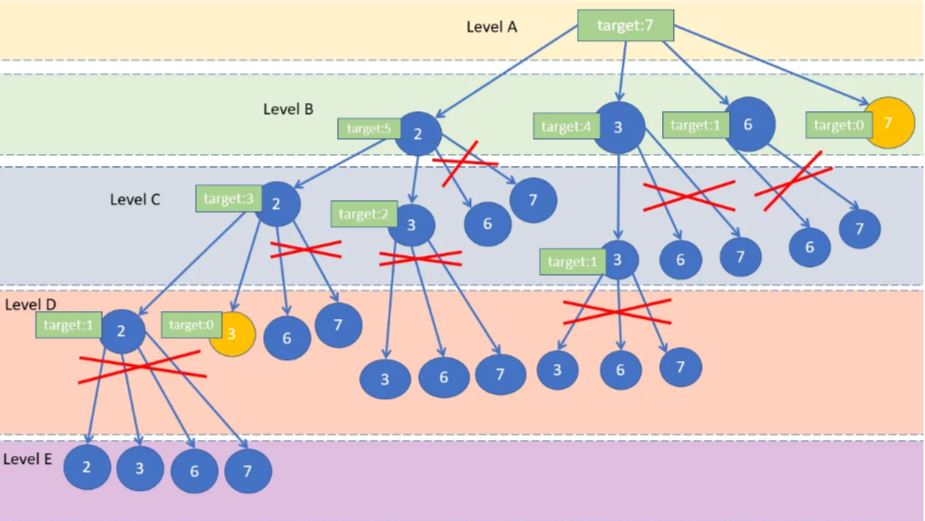
一樣推薦把 recursion Tree 畫出來幫助思考。
寫一個 dfs 遞歸函數,並說明 function 的一些狀態變量:- inner: 用 inner 來裝,<到目前為止,所選的所有數字>
- target: 每次調用新的 dfs 遞歸函數時,此時的 target 要減去目前選到的數字
- level: 記錄當前的遞歸到的 for loop 下標,用來避免計算到只是排列不一樣的 combination
一開始解題時,我並沒有寫 level 這個參數,故 dfs function:
public void dfs( int[] candidates, Deque<Integer> inner, int target ) {
if ( target == 0 ) {
ans.add( new ArrayList<>( inner ) );
return;
}
for ( int num : candidates ) {
if ( num > target ) {
return;
}
inner.push( num );
dfs( candidates, inner, target - num );
inner.pop();
}
}
但這會導致出現重複組合,例如[2,3,6,7];target=7,答案會變成 [[3,2,2],[2,3,2],[2,2,3],[7]],其中[[3,2,2],[2,3,2],[2,2,3]為重複的組合,它們視為同個 combination,只是順序不一樣。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> combinationSum( int[] candidates, int target ) {
Arrays.sort( candidates );
dfs( candidates, new ArrayDeque<>(), target, 0 );
return ans;
}
public void dfs( int[] candidates, Deque<Integer> inner, int target, int level ) {
if ( target == 0 ) {
ans.add( new ArrayList<>( inner ) );
return;
}
for ( int i = level; i < candidates.length; i++ ) {
if ( candidates[i] > target ) {
return;
}
inner.push( candidates[i] );
dfs( candidates, inner, target - candidates[i], i );
inner.pop();
}
}
}
時間空間複雜度
假設 candidates 有 m 個元素小於 target :
時間複雜度 : O(d*m^d);d = target/min[candidates]
Backtrack 時間複雜度,會由 Recursion tree 的 Node 個數和 Node 行為決定。
Node 個數 :
- 第一次調用遞迴,因為我們有
candidates[i] > target 返回這個條件,所以第一層只會有 m 個 Node- 第二次調用遞迴,我們 target 會變小,且還是有
candidates[i] > target 返回這個條件,所以小於 target 的元素個數,會比上一層 m ,還要再少一些,假設 m_1,所以第二層會有 m*m_1 個 Node- …
承上可知總數為:
m + m*m_1 + m_1*m_2 + ... + m_(d-1)*m_d ; d 為最大深度。但由於每一層的 target 都在變小,故 m series 也都遞減。故簡化一下,假設每層都是最大值 m 個 Node ,這邊是取最大值。再來 Recursion tree 的深度也很難估計,故用最大深度
target / min[candidates] = d來表示整個 Recursion tree 的深度,這邊也是取最大值。承上分析,Node 個數有 :
- 第一層:
m = m^1- 第二層:
m*m = m^2- …
- 第 d 層:
m*....*m = m^d使用等比級數和公式,總共
m(1-m^d)/(1-m) ~ m^d個。
Node 行為 :
- 非葉子節點: 只有插入和移除元素的操作,都是常數級的。
- 葉子節點: 會有複製 List 的操作,因為最大深度為 d,故所有 List 內最多
d個元素,複製需要O(d)時間。這邊就假設所有 Node 行為都需要花
O(d)時間來做事,這邊也是取最大值。
承上所有分析,時間複雜度為:
O(Node個數*Node行為) = O(d*m^d),其中d = target / min[candidates]
空間複雜度 : O(d) ;d = target/min[candidates]
Recursion tree 深度優先搜索(DFS)會產生一個 recursion stack ,而 Recursion tree 的深度很難估計,故用最大深度 target / min[candidates] = d來表示吧。再來 code 有一個 for 迴圈,沒有創建額外的存儲空間,故每個 Node 還是常數空間複雜度。
總結以上,故空間複雜度為(深度 * 常數空間): O(d*1)=O(d)
補充
其實<假設 candidates 有 m 個元素小於 target> 還蠻巧妙的…。這邊可以參考 leetcode 40. 的時間複雜度分析。我們把 array 補到<如果重複使用,最多可以用幾次>的個數,再假設數字也不能重複使用,以上思想在排列組合上,會等同於原本題目可以重複使用的情況 !
例如實際範例 :
int[] candidates = {2, 3, 4, 5, 6}
把它轉變成 leetcode 40. combination sum II 要求的條件,就變成 :
int[] new_candidates ={2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 6, 6},再加上每個元素只能用一次
這樣就可以使用 leetcode 40. 方式來分析時間複雜度: O(N*N!); N = length(new_candidates)。特別注意 N 是代表延長過後的 array 長度。