46. Permutations
是一道經典 distinct integers 的全排列問題,這邊使用 Backtrack 來求解。從數學上來說,n 個 element 的 Permutation 一共有 n! 種排序,思考起來算蠻簡單的,但要用程式模擬這個推導過程,卻是有點難度的,因此被歸類在 Medium 等級。
思路
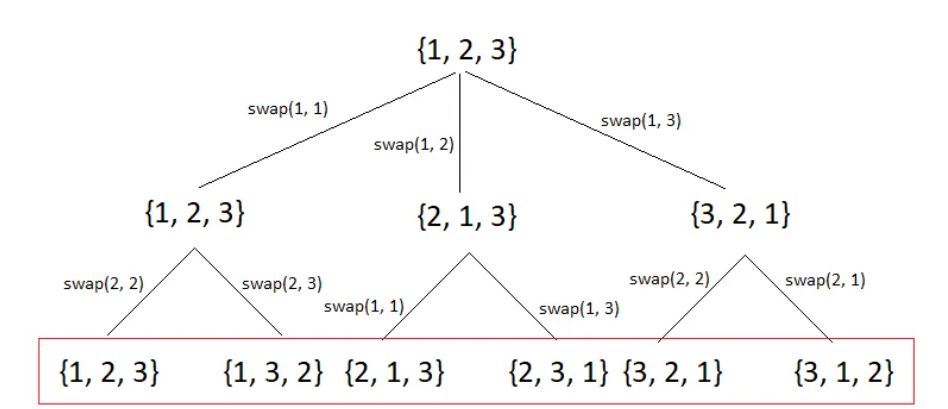
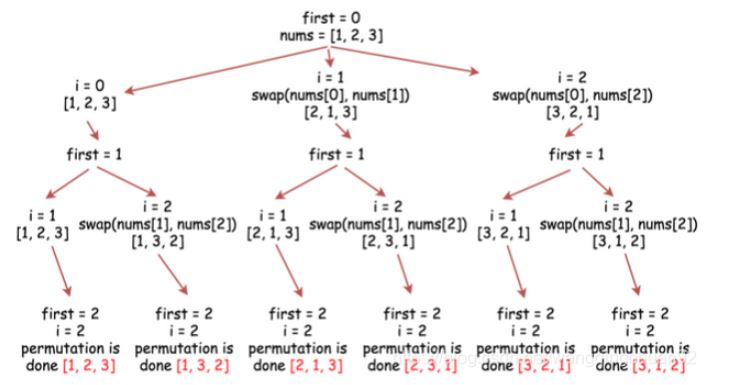
推薦把 recursion Tree 畫出來幫助思考。另外這邊使用一個比較巧妙的方法,用交換 num 裡面的兩個數字的方式,之後做 DFS ,經過遞迴可以產出所有的排列情況。
最高層的問題就是我們的原始 input,而 State 設計,用位置 index 做為參數。第一層做完就會確定第一個位置的數字,有 nums.length 種可能性;第二層做完就會確定第二個位置的數字,有 nums.length - 1 種可能性,以此類推…
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
dfs(nums, 0);
return ans;
}
private void dfs(int[] nums, int depth){
if(depth >= nums.length){
List<Integer> res = new ArrayList<>();
for(int num : nums){
res.add(num);
}
ans.add(res);
return;
}
for(int i = depth ; i < nums.length ; i++){
swap(nums, depth, i);
dfs(nums, depth + 1);
swap(nums, i, depth);
}
}
private void swap(int[] nums, int i, int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
一般這種 Top Down DFS 問題都是 return void 的; bottom up DFS 才會有 return 具體的 type。
因為 java object 是存地址,故要把當前答案做一個 copy
List<Integer> res = new ArrayList<>();
for(int num : nums){
res.add(num);
}
ans.add(res);
目前 java 沒有天然提供 int[] 轉 List<Integer> 的 util,所以用最樸直的方式來轉換。
swap(nums, index, i);
dfs(nums, index + 1);
swap(nums, i, index);
代表狀態的 backtrack,讓其他分支狀態不互相干擾。
時間空間複雜度
由上圖幫助思考,假設 nums 有 N 個元素 ,深度 depth 代表的節點狀態的定義是 : 該位置的元素要和其 index 大於等於自己的位置的元素 swap :index 等於自己的位置的 swap,代表沒有交換的狀態,這也是一種情形。
時間複雜度 : O(N*N!)
Backtrack 時間複雜度,會由 recursion tree 的 Node 個數和 Node 行為決定。因為演算法在葉子節點和非葉子節點的行為不一樣,所以分開計算 :
非葉子節點
- 在 depth 深度為
0時,代表index = 0的元素要和index = 0 到 index = N個元素交換,這代表 recursion tree 這層會有 N 個節點。- 在 depth 深度為
1時,代表index = 1的元素要和index = 1 到 index = N個元素交換,這代表 recursion tree 這層會有 N - 1 個節點。- …
推理一下,可發現 recursion tree 的非葉子節點個數總共有,
N + (N-1) + ... + 1 = (1+N)N/2且每次 swap 的時間複雜度為常數,故非葉子節點時間複雜度為O(N^2)。
葉子節點
關於葉子節點,我們用高中數學知道其數量就是
N!,然後因為要拷貝成一個新的 array 需要的時間複雜度是O(N),故葉子節點總共時間複雜度為O(N*N!)
最後總體看一下,影響最大的是葉子節點,故總體時間複雜度是O(N*N!)。但實際上速度會比 O(N*N!) 還要好一點,因為非葉子節點速度比 O(N*N!) 還要快。
空間複雜度 : O(N)
recursion tree 深度優先搜索(DFS)會產生一個 recursion stack ,其深度剛好就是 N 。再來 code 有一個 for 迴圈作用是遍歷 index 然後 swap 數字和觸發遞迴呼叫,這些都只是 in-place 操作,沒有創建額外的存儲空間,故每個 Node 還是常數空間複雜度。
總結以上,故空間複雜度為(深度 * 常數空間): O(N*1)=O(N)