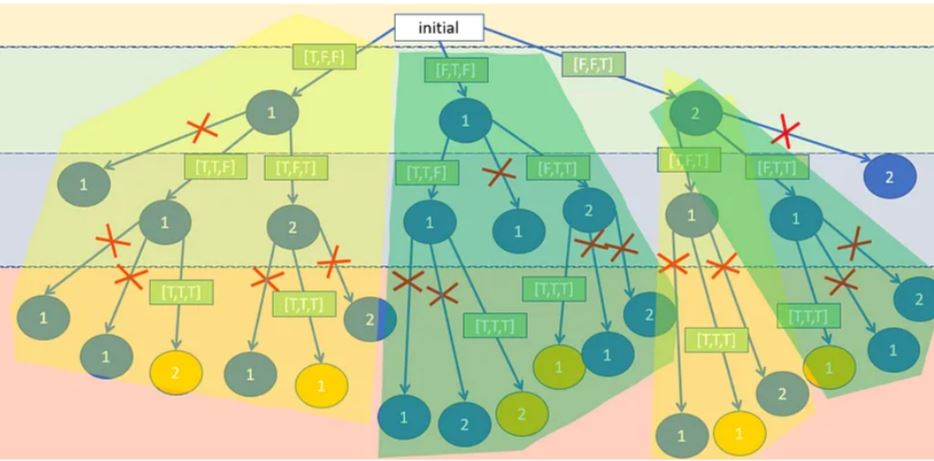
Permutations 另解
之前解題利用了交換 nums 裡面的兩個數字的方式,這次換另一種寫法,做出一個 inner list 收集可能的結果。基本解題思想都還是 Backtracking ,故把 leetcode46 和 leetcode47 重新解答一遍。
思路
Backtracking 的思路,就是一直作選擇,再根據做的選擇,去做下一個選擇,直到已不能再做選擇為止,這時就會取消我們做的前一個選擇,並回到選擇前的狀態,再改選另一個…,直到試過每個可能的選擇組合。
46. Permutations
本題所有數字都保證是不重複的。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
boolean[] visited = new boolean[nums.length];
dfs(nums , new ArrayList<>(),visited);
return ans;
}
public void dfs(int[] nums, List<Integer> inner, boolean[] visited){
if(inner.size() == nums.length){
ans.add(new ArrayList<>(inner));
return;
}
for(int i = 0 ; i < nums.length; i++){
if(visited[i]){
continue;
}
visited[i] = true;
inner.add(nums[i]);
dfs(nums, inner, visited);
inner.remove(inner.size() - 1);
visited[i] = false;
}
}
}
用一個 boolean array 去紀錄 到底有沒有過這個數字,本例是用 visited[i] 就代表,有無選過 nums[i]
47. Permutations II
承 46. Permutations,如果用同樣的程式來求解 [1,2,2] 的全排列 :
Expected:
[[1,1,2],[1,2,1],[2,1,1]]Actual:
[[1,1,2],[1,2,1],[1,1,2],[1,2,1],[2,1,1],[2,1,1]],會得到很多長得一模一樣的inner list
要怎麼避免重複的 inner list 呢?
- 先把數字排列好順序,因此一樣數字會聚集在一起。
- 再來檢查現在 index 的數字,是不是跟前一個位置的數字一樣:
- 跟前一個位置的數字不一樣的話,就正常 backtrack
- 跟前一個位置的數字一樣的話,再檢查有沒有已經把前一個 index 的數字加進陣列了
- 不是的話,就跳過,換下一個
- 是的話,就可以執行正常 backtrack
上述來蠻繞口的,舉例來解釋 [1,1,2]:
nums[0 ]的 1 跟 nums[1]的 1 當作不同的東西。這裡我們先表示為 nums[0] = 1 跟 nums[1] = 1' 。但針對全排列, nums[0] = 1 跟 nums[1] = 1' 的排列,是一模一樣的,所以針對這個來制定一個規則:如果數字一樣的話,index 比較小的,一定要先出現,否則不接受該數字
規則在範例[1,1,2]來說,就是1一定要比1'早出現。用這樣的規則的話,針對更多個重複數字,比如有多個 1 重複,例如 [1,1,1,2],這裡我們先表示為 nums[0] = 1 、nums[1] = 1' 、nums[2] = 1'' ,則 1一定要比1'早出現,而1'一定要比1''早出現。
所以最前面先把數字排列好順序很重要,相同數字才會聚集在一起,才能用visited[i-1]來判斷。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
boolean[] visited = new boolean[nums.length];
dfs(nums, new ArrayList<>(),visited);
return ans;
}
public void dfs(int[] nums, List<Integer> inner, boolean[] visited){
if(inner.size() == nums.length){
ans.add(new ArrayList<>(inner));
return;
}
for(int i = 0 ; i < nums.length; i++){
if(visited[i]){
continue;
}
if(i!=0 && nums[i] == nums[i-1] && !visited[i-1]){
continue;
}
visited[i] = true;
inner.add(nums[i]);
dfs(nums, inner, visited);
inner.remove(inner.size() - 1);
visited[i] = false;
}
}
}
在把 inner list 加進 ans 前,檢查 ans 內有沒有加過一模一樣的 inner list,這方式也是可以避免重複的inner list。但會非常浪費時間,因為要去蒐集所有可能的答案,最後才判斷。
時間空間複雜度
假設 nums 有 N 個元素:
時間複雜度 : O(N*N!)
參考原本 46、47 題時間複雜度分析,這題雖然換個寫法,47 還多了個排序,但主要影響時間複雜度分析的,仍然還是葉子節點,故時間複雜度兩題都還是O(N*N!)
雖然有 array 排序的演算法複雜度 O(NlogN),但不影響整個時間複雜度分析。
空間複雜度 :O(N)
參考原本 46、47 題時間複雜度分析,且新寫法在 47 題,並不需要一個新的 set 來檢查重複,故兩題空間複雜度都是O(N)