47. Permutations II
是經典的 46. Permutations 的進階版,現在數字會有重複(duplicate) 。這邊一樣使用 Backtrack 來求解。從數學上來說,
n個 element ,且將相同的事物歸為一組, 可歸成 k 組, 且每組有m_i個,其 Permutation 一共有n!/(m_1!m_2!...m_k!)種排序,為高中數學題中,需要思考下的題目;用程式模擬這個過程也有難度,故被歸類在 Medium 等級。
思路
承前面 46. Permutations 解法,用交換 num 裡面的兩個數字的方式來做 DFS ,基本上 code 幾乎都一樣,但多加入檢查重複的機制。
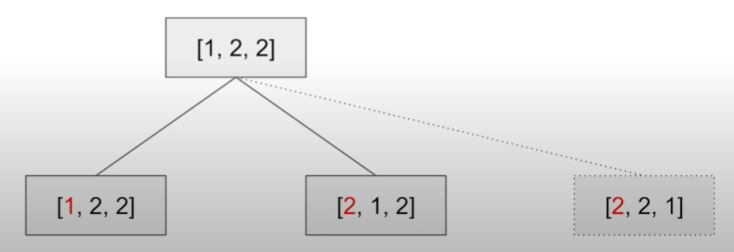
思考上面的圖時,可能初次會覺得 [2,1,2] 和 [2,2,1] 這兩個狀態是完全不一樣。但看再下一層的狀態,[1,2]、[2,1] ,這兩個的全排列其實是一樣的。
所以在嘗試所有可能性時,必須檢查如上圖產生的重複部分,故在這邊是利用 hashset 來檢查重複,把發現已經嘗試過的元素而產生的重複 branch 給剪除掉。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
dfs(nums, 0);
return ans;
}
private void dfs(int[] nums, int index){
if(index >= nums.length){
List<Integer> res = new ArrayList<>();
for(int num : nums){
res.add(num);
}
ans.add(res);
return;
}
Set<Integer> set = new HashSet<>();
for(int i = index ; i < nums.length ; i++){
if(set.add(nums[i])){
swap(nums, i, index);
dfs(nums, index+1);
swap(nums, index, i);
}
}
}
private void swap(int[] nums, int i, int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
java 的小技巧, set 的 add 函數有 bool 回傳值,可把 code 做簡化。
攏長寫法:
if(set.contains(nums[i])){
continue;
}
set.add(nums[i]);
swap(nums, i, index);
dfs(nums, index+1);
swap(nums, index, i);
時間空間複雜度
假設 nums 有 N 個元素 :
時間複雜度: O(N*N!)
承前面 46. Permutations 分析,知道時間複雜度是O(N*N!)。但實際上速度還會更好,因為有去除重複,故 recursion tree 基本不會需要整個遍歷完全。
雖然有 array 排序的演算法複雜度 O(NlogN),但不影響整個時間複雜度分析。
空間複雜度:O(N^2)
recursion tree 深度優先搜索(DFS)會產生一個 recursion stack ,其深度剛好就是 N 。再來每一層中,都會有一個 set ,而這個 set 最多可以存 N 個元素,故空間複雜度為(深度 * set空間): O(N*N)=O(N^2)