最長回文子串 (Longest Palindromic Substring) 是常考題。Palindrome 就是正讀反讀都一樣的詞語，比如範例給的 “bab”、 “bb” ，實際單字如 “level” 等等都屬於它。因為較好的解法是 DP 類型，初見就能想到，難度也比較高。一般人能熟悉 Dynamic Programming - 2D matrix 解就好了。(看過令人膜拜的神解 Manacher’s Algorithm，時間複雜度提升到了 O(n) …)

思路

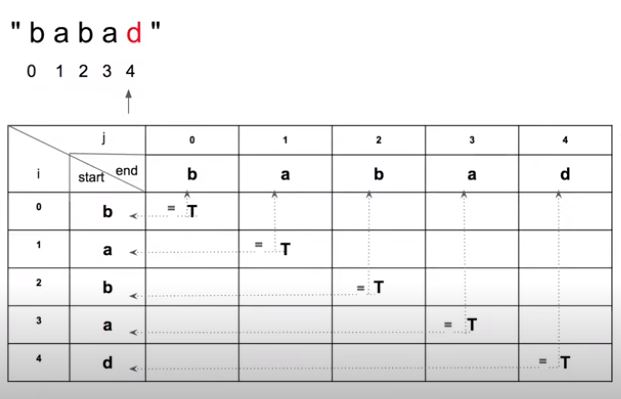
我們維護一個 2D-Matrix 動態紀錄子問題狀態，其中 dp[i][j] 表示字符串區間 [i, j] 是否為回文串。明顯地，當 i = j 時，表示只有一個字符，肯定是 Palindrome ，故先把對角線表填完 T (如上圖) 。

再來是 Palindromic 字串的特性，若字串最兩端點一樣，則 dp[i+1][j-1]表示內縮一層的單字，

也必定是 Palindromic 字串。可利用這個特性寫出狀態方程式 dp[i][j] = dp[i + 1][j - 1];

再來特別注意 Palindromic 字串在 DP 表格之間的依賴關係很特別，故for loop 時候必須:

// 特別注意 i,j 寫法及順序!!

for(int j = 1 ; j < length ; j++){
    for(int i = 0; i < j ; i++){
        ...
    }
}

for(int i = length - 1 ; i >= 0 ; i--){
    for(int j = length - 1; j >= i ; j--){
        ...
    }
}

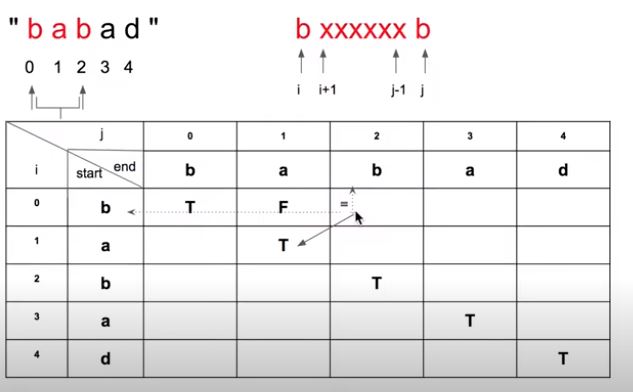
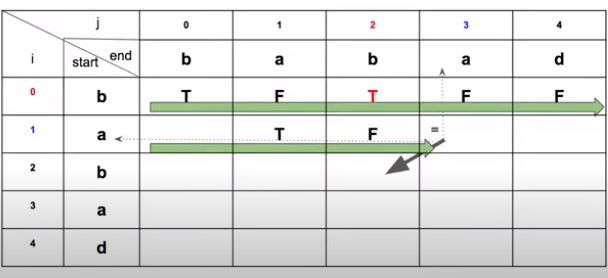
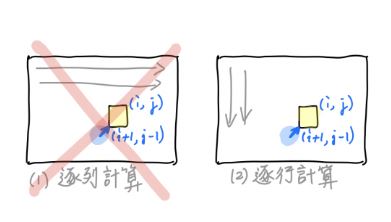
因為在判斷 dp[i][j] 時，需要先有 dp[i+1][j-1] 的資訊，要不然會出錯 ! 錯誤的原因如下圖箭頭處所表示。

所以 loop 的方式有所限制 :

  • 順序逐 row 計算會出錯

解答

class Solution {
    public String longestPalindrome(String s) {
        if ( s.length() == 1 ) {
			return s;
		}
		String ans = s.substring( 0, 1 );
		int maxLength = 1;
		int length = s.length();
		boolean[][] dp = new boolean[length][length];

		for ( int i = 0; i < length; i++ ) {
			dp[i][i] = true;
		}

		for ( int j = 1; j < length; j++ ) {
			for ( int i = 0; i < j; i++ ) {
				if ( s.charAt( i ) == s.charAt( j ) ) {
					if ( j - i < 2 ) {
						dp[i][j] = true;
					} else {
						dp[i][j] = dp[i + 1][j - 1];
					}
				}

				if ( dp[i][j] && j - i + 1 > maxLength ) {
					maxLength = j - i;
					ans = s.substring( i, j + 1 );
				}
			}
		}

		return ans;
}

j-i <= 2 的理由是因為前面判斷了 s.charAt(i) != s.charAt(j)，故子字串只要長度小於等於 2 ，就一定是回文。再來只要 dp[i][j] == true，就表示 s.substring(i, length) 是回文。其中長度是 j-i+1 。

時間空間複雜度

時間複雜度 : O(N^2)

兩層迴圈

空間複雜度 : O(N^2)

2-D矩陣，為了紀錄某步驟執行結果(動態規劃)

Vocabulary

palindrome [ˋpælɪn͵drom] (只會出現在考題的單字，記得怎麼念就好)

n.[C] 回文字

參考資料