這題是非常有名的 Fibonacci 數列，其特徵是除了前兩個數字之外，每個數字等於前兩個數字之和。解法可以帶出一些經典觀念和想法，例如 :

• Dynamic Programming
• 迭帶 for-loop
• recursion 遞迴

由於 Fibonacci 數列的時間空間複雜度計算比較特別，加上可以很初步引入很多的思考方式，故雖然這題是 easy ，我還是做個紀錄。

解答

迭帶 for-loop

可使用長度固定的 Array 來儲存運算過程中的答案。而這個儲存想法就是 動態規劃 Dynamic Programming。建立一個大小為 N+1 的 dp Array，其中 :

• dp[i] 為位置 i 上的數字
• 先初始化前兩個分別為 0 和 1
• 狀態轉移方程式就是斐波那契數組的性質: dp[i] = dp[i-1] + dp[i-2]

class Solution {
    public int fib(int n) {
        if(n <= 1) return n;

        int[] dp = new int[31];
        dp[0] = 0;
        dp[1] = 1;

        for(int i = 2 ; i <= n ; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }

        return dp[n];
    }
}

上面解法可進行空間上的優化，由於 Fibonacci 的第 n 項，只跟前兩項有關，所以不需要保存整個 Array，因此可以 :

class Solution {
    public int fib(int n) {
        if( n <= 1 ) return n ;

        int a = 0;
        int b = 1;

        for(int i = 2 ;  i <= n ; i++){
            int sum = a + b;
            a = b;
            b = sum;
        }

        return b;
    }
}

recursion 遞迴

屬於逆向思維，從最終想要的答案出發，逐步往前尋找答案，並且用它們構造當前的答案。

class Solution {
    public int fib(int n) {
        if( n <= 1 ) {
            return n ;
        }

        int tmp1= fib( n - 1 );
        int tmp2 = fib( n - 2 );

        return tmp1 + tmp2;
    }
}

看了 Fibonacci 數列，發現可以用迭代 for-loop 或遞迴 recursion 的方法解決。 而且看起來迭代的方法，似乎更加簡潔優雅，那麼 :

我們為什麼要學 recursion 呢 ? 難道不能只用 for-loop 嗎 ?

答案是不可以，因為某些問題很難用 for-loop 的方式來實現，但 recursion 卻可以很簡潔的實現。 例如歸併排序 Merge Sort 就是個很好的例子。

時間空間複雜度

時間複雜度 : O(((1+根號5)/2)^N)

承之前文章 Recursion Template 的步驟分析 :

• Base case處理 : O(1)
• 構造當前層答案 : O(1)

故 Fibonacci 的時間複雜度為: O(節點個數)，那麼這棵遞歸樹有多少個節點呢 ?

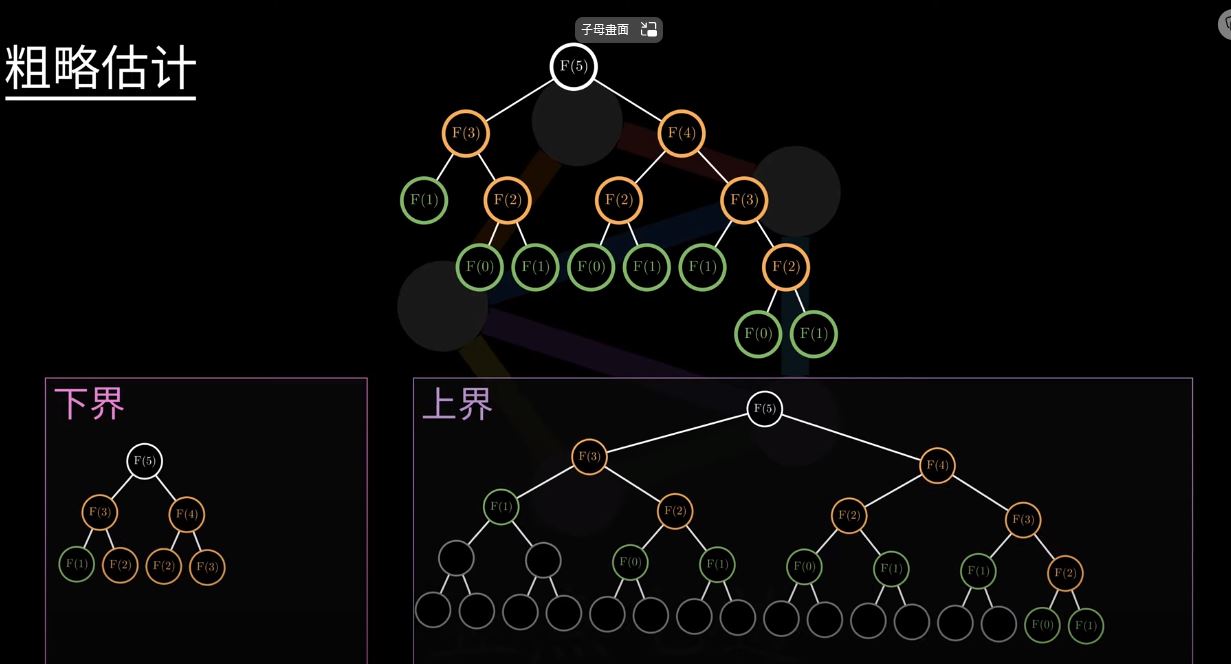
粗略估計

• 下界的 tree: 隨著每層的深入，n 每次會減少 2，直到減小到 1 或 0，因此高度為: (n+1)/2 向上取整 ~ n/2
• 上界的 tree: 隨著每層的深入，n 每次減小 1，故高度為 n

因為高度為 n 的 binary tree 節點個數，公式為 2^n-1，故 Fibonacci 時間複雜度處於O(2^(N/2))與O(2^N)之間。

精確計算

首先觀察 Fibonacci 數列可以發現，Fibonacci 數列都乘以2，然後再減 1，就剛好和前一個節點數一樣，可以透過數學歸納法證明，因此精確的節點個數: 2*F[n+1]-1

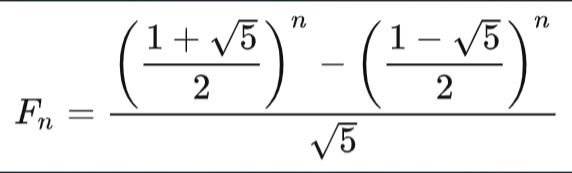
再來 Fibonacci 是有通用公式的

帶入到精確的節點個數的算式，最後可以得到精確答案 O(((1+根號5)/2)^N)

空間複雜度 : O(N)

即為 Recursion tree 高度，為 O(N)

參考資料

• [LeetCode] 509. Fibonacci Number 斐波那契数

• 【递归3】递归树与时间复杂度