78. Subsets
很經典的問題 : 冪集 the power set ,在數學上還蠻常見到的,理論上求得解答方式也很簡單,選或者不選排列組合,就可以得出答案。但在程式上要實現卻有一點點難度,故會被歸類到 Medium 等級。這邊使用 Backtrack 模板來解題。
思路
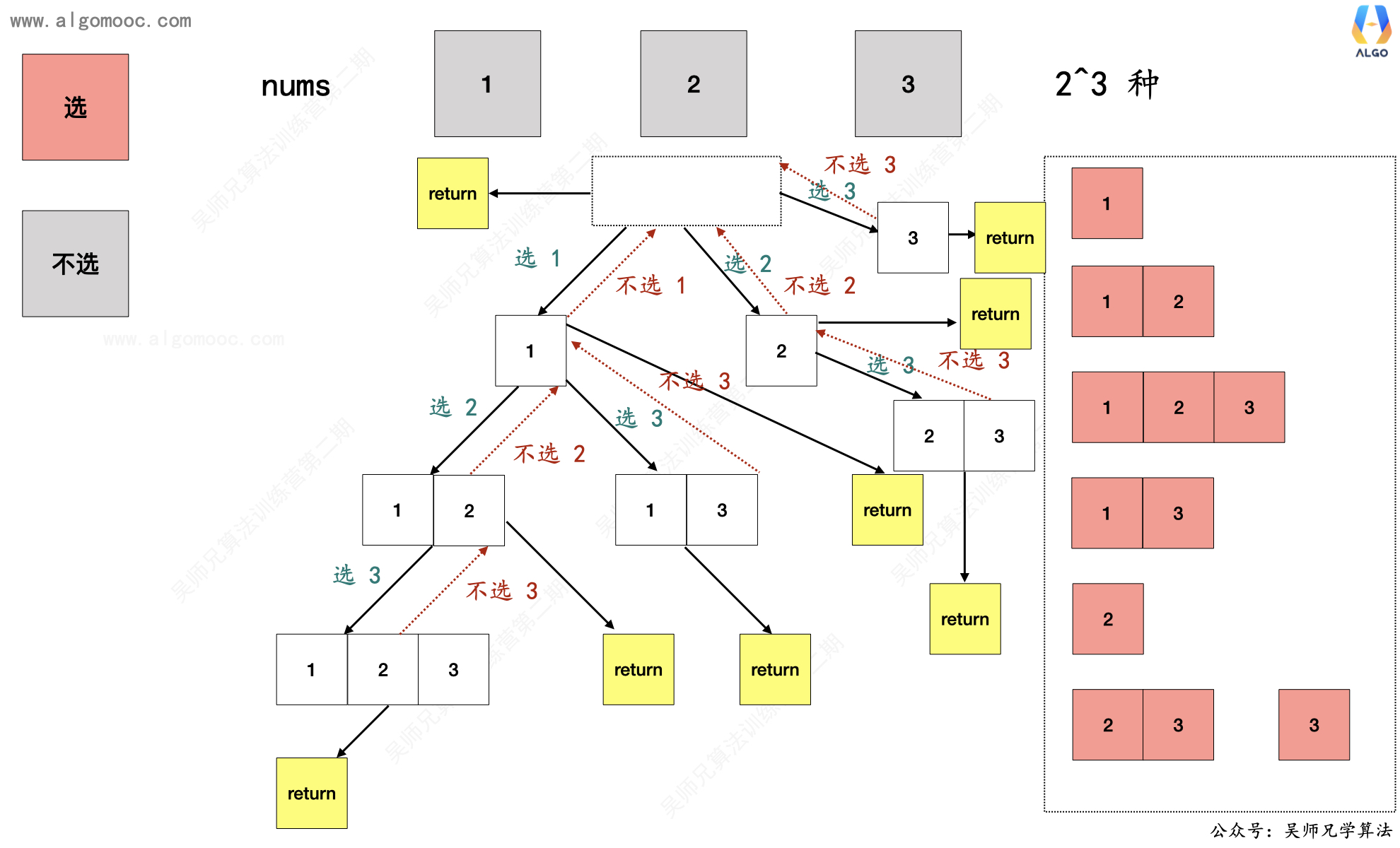
冪集是要蒐集所有 subset,這裡表示的方式是,把每一層 inner list 狀態都保存下來。注意一個很重要的假設: nums 中的數字各不相同,故可以不用思考數字重複的情況,所有答案都收集起來也不會有重複的 case。構造 tree 如下圖 :
注意空集合 [] 也是一個 subset,但是這不是特殊 case,全部都不選就是 empty subset 了
Subset 類別題目和 Permutation 題目不一樣的點,在於其需要在 tree 的所有節點,執行加入結果集這操作,而全排列只需要在葉子節點執行就可以了。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> subsets( int[] nums ) {
dfs( nums, new ArrayList(), 0 );
return ans;
}
public void dfs( int[] nums, List<Integer> inner, int level ) {
ans.add( new ArrayList( inner ) );
for ( int i = level; i < nums.length; i++ ) {
inner.add( nums[i] );
dfs( nums, inner, i + 1 );
inner.remove( inner.size() - 1 );
}
}
}
時間空間複雜度
假設 nums 有 N 個元素:
時間複雜度: O(N*2^N)
Backtrack 時間複雜度,會由 recursion tree 的 Node 個數和 Node 行為決定。
- Node 個數即為所有 subset 個數:
2^N - Node 行為,主要是複製 List ,這邊就以可能複製的最長的 List,取花費時間的上限:
O(N)
最後總體看一下,假設每個 Node 都花費最長O(N)時間,則時間複雜度:O(N*2^N)
空間複雜度:O(N)
recursion tree 會產生一個 recursion stack ,其最深度剛好就是 N 。再來 code 沒有創建額外的存儲空間,故每個 Node 還是常數空間複雜度。
總結以上,故空間複雜度為(深度 * 常數空間): O(N*1)=O(N)