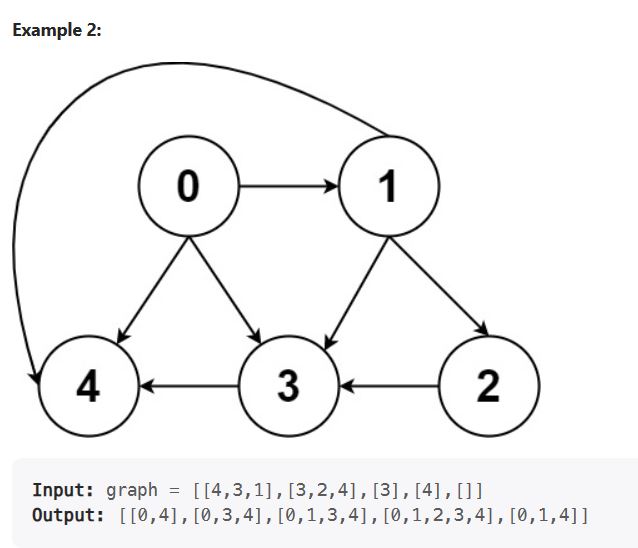
797. All Paths From Source to Target
這題給了我們一個無環有向圖 (directed acyclic graph)(DAG) 。有 N 個 node ,要找出所有可能的從
node 0到node N-1的路徑。像這種需要走到終點,且在每一次新的遞迴時,都要把當前路徑記錄下來,其本質都是深度遍歷 graph ,再加上 backtrack 回溯狀態。是經典的 dfs 的題目。
思路
一開始 input 資料的意思有些難懂,這裡來看例子中 [[1,2], [3], [3], []] ,其每個小 array 代表當前 node 可相通的鄰 node。即 :
node 0的鄰結點是node 1node 2
node 1的鄰結點是node 3
node 2的鄰結點是node 3
這樣再來看其他範例應該就明顯知道徒的意思了 :
接下來使用 dfs 來遍歷並記錄 node ,其終止條件是達到最後目標點,即是到達結點node N-1,則將其 path 加入結果 res。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
Deque<Integer> path = new LinkedList<>();
path.push(0);
dfs(graph, path, 0);
return ans;
}
private void dfs(int[][] graph, Deque<Integer> path, int node){
if(node == graph.length - 1){
List<Integer> list = new LinkedList<>(path);
Collections.reverse(list);
ans.add(list);
return;
}
for(int point : graph[node]){
path.push(point);
dfs(graph, path, point);
path.pop();
}
}
}
這裡使用 Deque<Integer> path = new LinkedList<>(); 可能不是個好選擇。
原本是想說可以方便使用 pop 來讓狀態回溯,但是在最後加入答案時,Deque 轉為 list 時候會是 stack pop 的順序,反向了 ! 所以多用 Collections.reverse(list); 來讓順用正確。或許直接只用 ArrayList 操作會更直覺。
Vocabulary
acyclic [eˋsaɪklɪk] : 注意發音,是[e] 不是 [ə]
adj. 非循環的;非週期的