90. Subsets II
是經典的 78. Subsets 的進階版,現在數字會有重複(duplicate)。這邊使用 Backtrack 模板來求解。這個題目還有要注意的地方,就是 array 不一定是順序的,例如 test case:
[4,4,4,1,4],這範例在我們去除重複答案的時候,若沒注意到有亂序的可能性,高機率會出錯。
思路
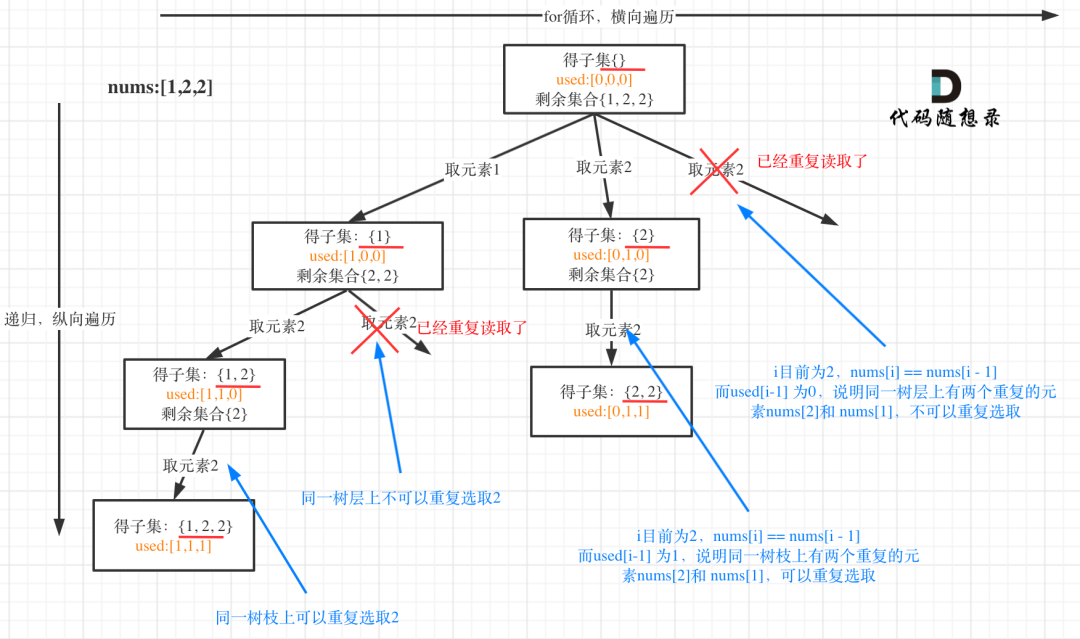
對於遞迴的解法,以[1, 2, 2]為例子,根據先前 tree 的模式,在處理到第二個 2 時,由於前面已經處理了一次 2,為了避免重複,我們只在添加加過第一個 2 的case,如 [2] 和 [1 2] ,後面添加 2 ,其他的 case 都不加。該如何實現前述的動作呢 ?if ( i != level && nums[i - 1] == nums[i] ) {
continue;
}
在 for loop 內補上上面的 code,就行了。如果當前元素 nums[i] 與前一個元素 nums[i-1] 相同,這代表在同一層級的處理過相同的值。因此,為了避免生成重複的子集,用nums[i - 1] == nums[i]來檢查是否需要跳過處理當前元素。
解答
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> subsetsWithDup( int[] nums ) {
Arrays.sort( nums );
dfs( nums, new ArrayList(), 0 );
return ans;
}
public void dfs( int[] nums, List<Integer> inner, int level ) {
ans.add( new ArrayList( inner ) );
for ( int i = level; i < nums.length; i++ ) {
if ( i != level && nums[i - 1] == nums[i] ) {
continue;
}
inner.add( nums[i] );
dfs( nums, inner, i + 1 );
inner.remove( inner.size() - 1 );
}
}
}
時間空間複雜度
假設 nums 有 N 個元素:
時間複雜度: O(N*2^N)
Backtrack 時間複雜度,會由 recursion tree 的 Node 個數和 Node 行為決定。
- Node 個數會因為有重複數字,而有剪枝的行為,導致數量會比所有 subset 個數還要少,這邊取最大值,即為 :
2^N - Node 行為,主要為複製 List ,這邊就以可能複製的最長的 List,取花費時間的上限:
O(N)
最後總體看一下,假設每個 Node 都花費最長O(N)時間,則時間複雜度:O(N*2^N)
空間複雜度:O(N)
recursion tree 會產生一個 recursion stack ,其最深度剛好就是 N 。再來 code 沒有創建額外的存儲空間,故每個 Node 還是常數空間複雜度。
總結以上,故空間複雜度為(深度 * 常數空間): O(N*1)=O(N)